In this article, I will explain what the term “inductive bias” means, where it can be found in machine learning, and why we need it. A little spoiler: inductive biases are everywhere. Every neural network has inductive bias (even the one in the human brain, heh-heh).

We will also cover the following:

  • Why inductive bias is a very good thing
  • Ways to implement inductive bias in machine learning models
  • What kind of inductive bias convolutional neural networks have and how the success of the Vision Transformer architecture is related to inductive bias

Let’s go!

What is inductive bias?

The term “inductive bias” has many definitions in the literature, all of which are informal. There is no formal definition, and the most rigorous possible one is based on formal mathematical logic. In this article, we will limit ourselves to the following definition:

Inductive bias is prior knowledge about the nature of the data that is somehow incorporated into a machine learning model.

To better understand the essence of inductive bias, let’s look at some examples:

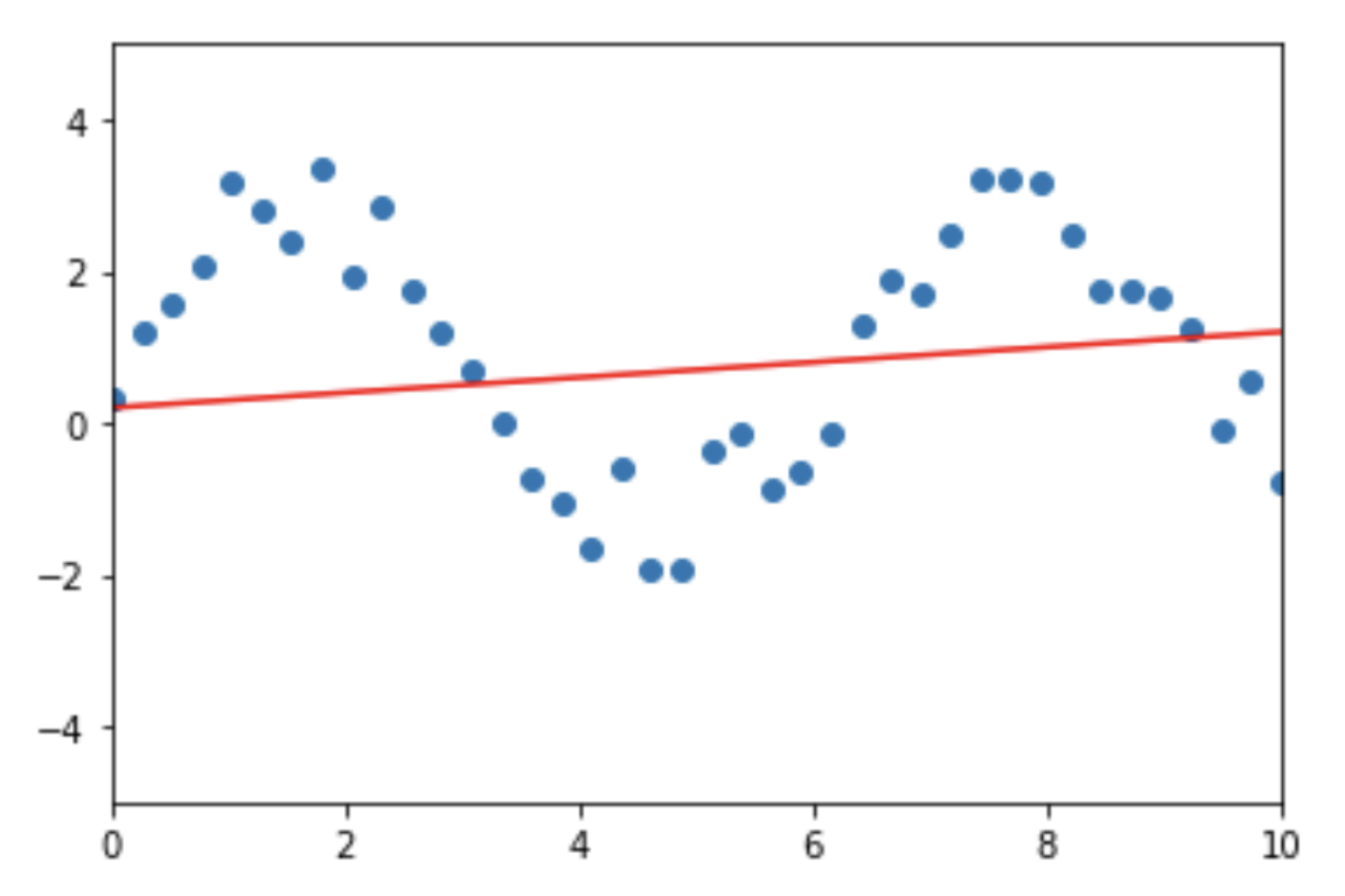
  1. Linear regression model. Linear regression is based on the assumption that there is a linear relationship between the target variable and the independent variables (features). The model is “embedded” with the knowledge that the data has a linear nature. Because of this limitation, linear regression poorly fits any data where the target variable does not depend on the features linearly (see the figure below). This assumption about the linear relationship between the features and the target is its “inductive bias” (more precisely, one of its inductive biases, as we will see later).
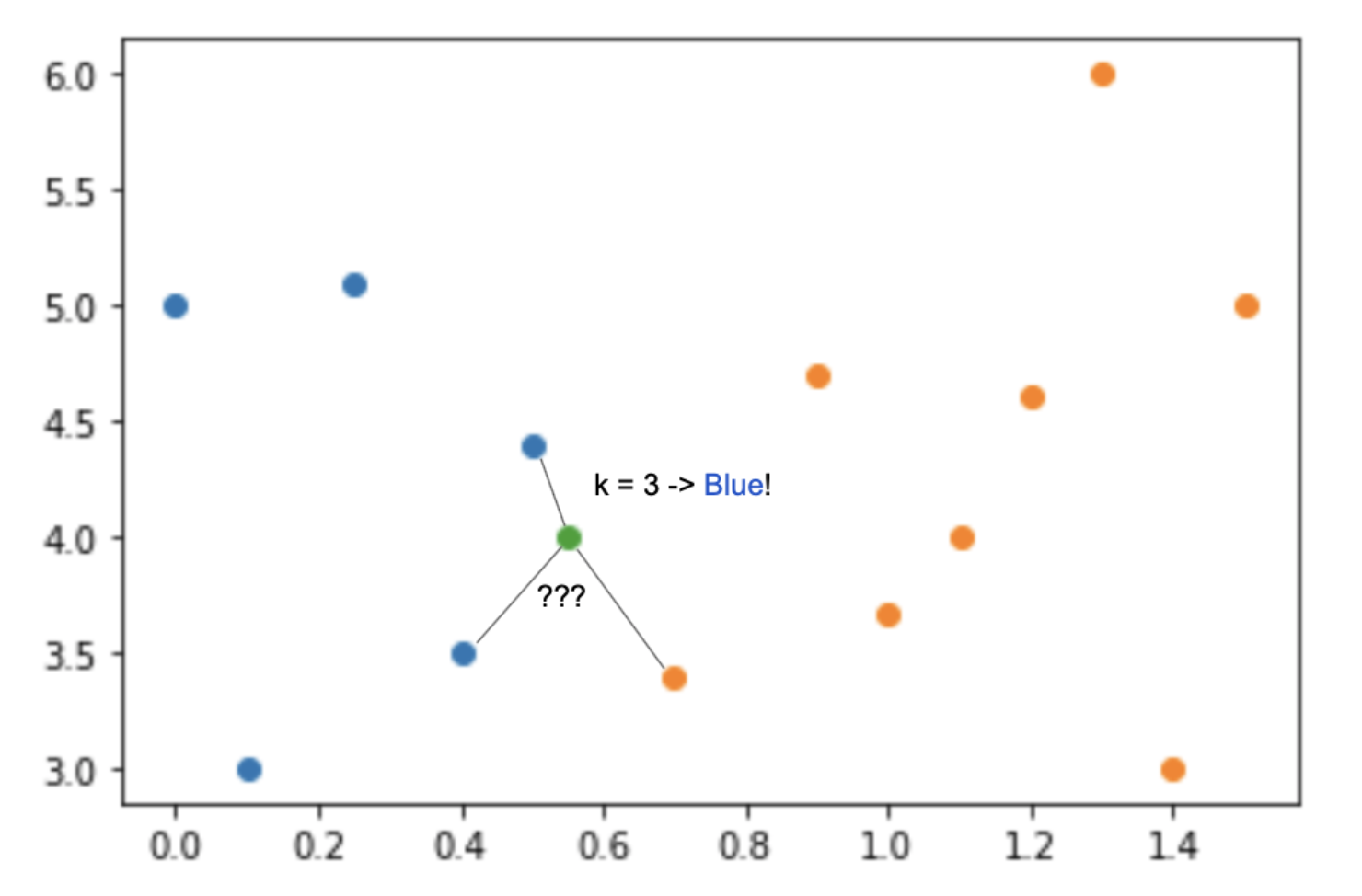
The X axis represents the feature value, the Y axis represents the target value. It is clear that the dependence of Y on X is nonlinear. Because of this, the Linear Regression model, which tries to build a linear dependence between X and Y, will fit this data very poorly.
  1. The K-nearest neighbors model. This model operates under the assumption of “compactness,” which means that “the value of the target variable for an unknown object is uniquely determined by the values of the target variables of the k objects closest (in some sense) to it.” This assumption is the “inductive bias” of the K-nearest neighbors algorithm. The KNN model is embedded with the knowledge that the target value for any object should be derived only from the target values of the closest elements of the training set to this object.
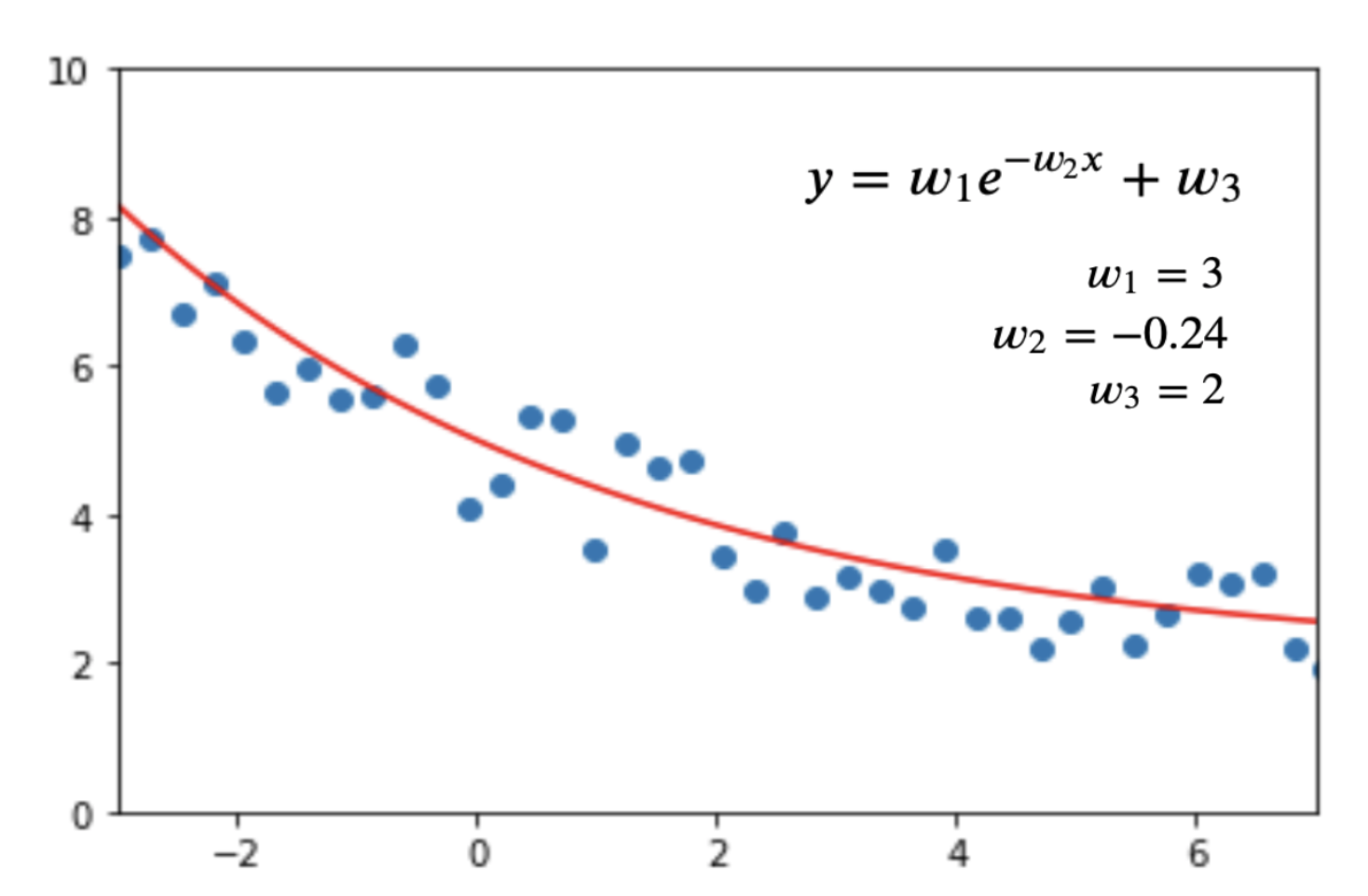
Illustration of object classification (green dot) by the KNN algorithm. Blue dots are objects of one class, orange ones are objects of another class. When k=3, the green dot will be assigned to the 'blue' class.
  1. Nonlinear regression. Let’s suppose we have data from some physical experiment. The data consists of two variables, \(x\) and \(y\). We would like to build a machine learning model that can predict the value of \(y\) given the value of \(x\). Furthermore, let’s say we know from theoretical physics that the equation for \(y\) as a function of \(x\) should be of a certain form: \(y= w_1 \exp(w_2 x) + w_3\). Then, all we have to do is train the machine learning model to find suitable values for the coefficients \(w_1\), \(w_2\) and \(w_3\) based on the collected data. We can do this, for example, using gradient descent (see the figure). This knowledge—that the machine learning model describing our data should express a function of the form \(y= w_1 \exp(w_2 x) + w_3\) — is the “inductive bias”.
Illustration of finding the optimal coefficients of the function y = w1*exp(w2*x) + w3 to describe the data (blue dots).

So, to summarize: Inductive bias refers to prior assumptions about the nature of the data that are somehow incorporated into a machine learning model, imposing restrictions on the form in which the model searches for the dependence of the target variable on the incoming data.

For now, we have considered rather trivial examples of inductive bias — those that are achieved by imposing restrictions on the model’s form itself. In general, one can “transfer” a priori knowledge to a model (i.e., endow the model with inductive bias) in different ways — not only by using a certain model architecture. We will discuss this below. But first, let’s note the following:

Inductive bias is inevitable

From the examples of Linear Regression and KNN, it may seem that inductive bias is a bad thing. After all, it limits the models! The inductive bias of Linear Regression prevents it from fitting well to data where there is no linear relationship between the target variable and the features. The inductive bias of the KNN algorithm prevents it from working well on data in which the target variable of an object is not uniquely determined by the values of the target variables of “close” elements. We see only disadvantages! So, is it possible to create a model without any restrictions?

But machine learning model cannot exist without inductive bias. And here’s why:

The goal of any machine learning model is as follows: using a training dataset, derive a general rule that will produce a target value for any element in the domain (not just elements in the training set). An example of such a task might be learning to solve a face recognition problem given 100,000 images of people’s faces, and then being able to recognize the face of any person in the world. This process of deriving a general rule for all elements in the domain based on a limited number of observations is called the generalization of a machine learning model.

https://bit.ly/31bvCvP

Such generalization is impossible without the presence of inductive bias in the model. Why? Because the training data is always finite. It certainly does not cover all possible observations in the real world. And from a finite set of observations, without making any additional assumptions about the data, a general rule can be derived in an infinite number of ways. After all, in general, the value of the target variable for elements outside the training sample could be anything.

Inductive bias is additional information about the nature of the data for the model; a way to show the model “which way to think”, what forms of solutions to consider, and what principle to base the generalization algorithm on. It allows the model to prioritize one method of generalization over another. It imposes certain limits on the model when choosing a generalization method, within which almost all generalization options will be quite adequate. The model becomes “biased” toward a solution of a certain type.

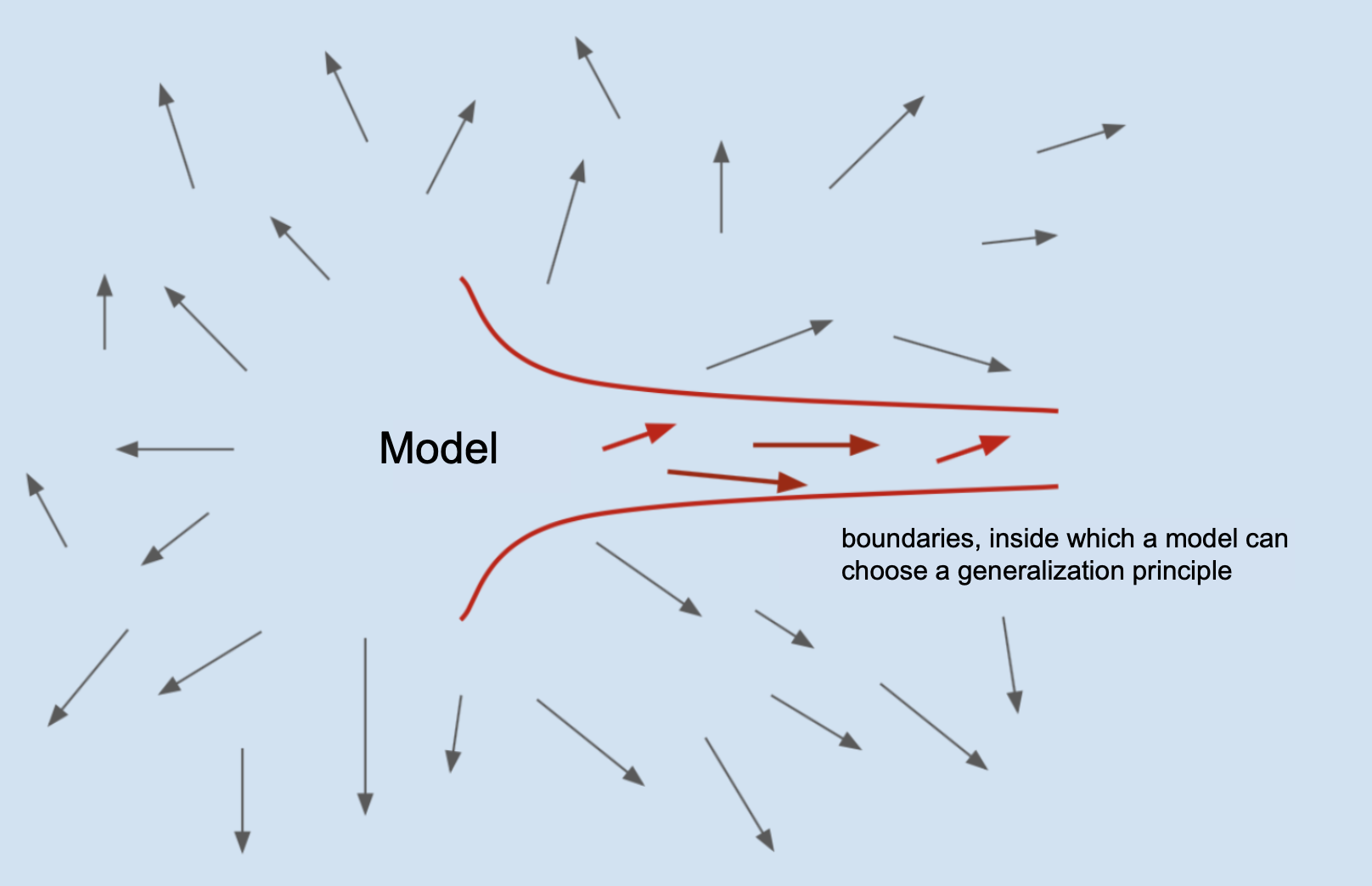
An illustration of how inductive bias imposes limitations on generalization ways to the model

For example, the inductive bias of Linear Regression forces the model to choose a solution form that has a linear nature. Similarly, the inductive bias of the model from the third example (nonlinear regression) tells the model that it is necessary to look for the dependence of the target on the input data in the form of a certain function, and the model only needs to select the appropriate parameters for this function.

When choosing a type of machine learning model for solving a specific problem, one needs to select a model whose inductive bias better fits the nature of the data and thus will help solve the problem more effectively. Generally speaking, the creation of new machine learning model architectures (for example, neural networks) essentially comes down to inventing an architecture that will have the suitable inductive bias to solve a specific problem.

So, we have understood that inductive bias is a good and useful thing. Let’s now discuss the ways in which inductive bias can be introduced into a model. We will see that manipulating the structure of the model architecture is just one of many ways to introduce inductive bias into the model.

Ways to introduce inductive bias into a model

Above, we’ve looked at examples of inductive biases in the models of Linear Regression and KNN. Both of these models have inductive biases “built into” the model architecture itself — into the very mechanism by which these models obtain the value of the target variable based on input data. We will now show that there are other ways to incorporate prior knowledge about the data into the model. To do this, let’s look at neural networks and the inductive bias in them.

First of all, each neural network has an architecture (structure). The architecture of a neural network consists of several components: the types of layers it has (fully connected, convolutional, recurrent, etc.), how many neurons are in each layer, what activation function is used in each layer, whether dropout and attention are used, and so on.

The architecture of a neural network determines the types of functions that the network can express. Indeed, a neural network is a function that describes the dependence of the output on the input, just like Linear Regression or the function \(y= w_1 \exp(w_2 x) + w_3\) from the nonlinear regression example above. But a neural network is a much more complex function, with a large number of trainable parameters and nonlinearities. Here it becomes clear that the architecture of a neural network is, in itself, its inductive bias.

Furthermore, each type of network layer — convolutional, fully connected, recurrent — has its own inductive biases, determined by the structure of these layers. Their inductive biases help them process the types of data they are designed for: images in the case of a convolutional layer, data presented as sequences in the case of a recurrent layer, and so on. We will talk more about the inductive bias of a convolutional layer below.

Next, the training algorithm of a neural network also imposes restrictions on the model. We train a neural network using the gradient descent algorithm, and not any other method. This also incorporates some knowledge into the model about how the preferred generalization method should be structured. Specifically, the gradient descent algorithm minimizes the average error of the model on the training samples using some loss function. That is, it forces the model to choose a method from all possible generalization methods that has the lowest average value of the given loss function on the training data.

It should now be clear that the choice of hyperparameters, such as the learning rate and the optimization algorithm (Adam, RMSProp, etc.), also contributes to the inductive bias: it forces the model to look for a way of generalization in a certain form.

Next, let’s consider the data. It is also possible to incorporate inductive biases through the training data (i.e., transfer knowledge about the data to the model via the data — heh-heh).

Here’s an example. Let’s say we are training a neural network to classify images of apples and pears. And let’s assume that in the training images, all the apples and pears are depicted in a vertical position:

By training a neural network on such data, we will most likely get a model that classifies images of rotated fruits poorly. This is easily explained: the model did not see a single fruit that was not vertical during training, so it simply did not learn to classify them. We want to avoid this and force the model to choose a generalization method that would allow it to successfully classify fruits rotated by any degree. To do this, we can change the training data: let’s augment it so that it contains images of rotated fruits.

When trained on such an augmented dataset, the model will be forced to choose the generalization method that will allow it to successfully classify not only vertical but also rotated fruit images.

Thus, we have introduced inductive bias into the neural network using dataset augmentation. Now, the training data and the neural network training algorithm (gradient descent) are designed in such a way that during training, the model “learns” that the data (pictures of fruits) can be not only located strictly vertically but also rotated by an arbitrary degree. And it learns to classify fruits rotated in different ways equally well.

Note that the required inductive bias (the understanding that fruit pictures are not only vertical) appeared in the model not only due to the presence of fruit pictures rotated by different degrees in the training dataset, but also due to the specific structure of the neural network training process. Gradient descent forces the neural network to learn to classify all pictures from the training dataset equally well, and therefore the neural network learns to classify rotated fruits as well.

This is an important point for understanding the essence of inductive bias because, most often, when talking about introducing inductive bias into neural networks, only manipulations with the neural network architecture and/or training data are mentioned. This happens because all neural networks are trained using gradient descent by default, and the role of this algorithm in introducing inductive bias into a neural network can be overlooked. However, without a specific structure of the training algorithm, manipulations with training data might not have the desired effect.

Let’s illustrate this with an example: imagine that we have changed the neural network training algorithm. Let’s say that instead of gradient descent, we use the following network training algorithm:

  • Select random values for the neural network parameters 100 times;
  • For each parameter set, calculate the value of the quality metric on the test dataset;
  • A “trained” neural network is one with parameters for which the best metric value was obtained on the test dataset.

Will this training method lead to good quality for the neural network in the classification task? And can we say that if we use this training method and add rotated fruit images to the training data, the network will certainly perform well on rotated fruit images? It seems that we can’t say “yes” for sure. Using such a training method, no amount of manipulation of the training data will particularly increase the probability of improving the algorithm’s performance.

Moreover, the neural network architecture itself plays a role in whether dataset manipulation will have the desired effect. For example, no matter how much inductive bias you introduce into the data and the training algorithm, you will never teach Linear Regression to be good at the face recognition task.

Thus, the introduction of any inductive bias into a machine learning model relies on certain characteristics of the model architecture, the training algorithm, and the training data. All of these factors influence how the model will generalize and what inductive bias it receives.

Sometimes, the restrictions that are imposed on a model to obtain a certain inductive bias do not have the expected effect. This happens because not all the features of the model structure, data, and training procedure were taken into account. In fact, most often, this is simply impossible to do. We will discuss this in the section where we examine the inductive bias of a convolutional neural network.

From this point in the post, we will assume that the gradient descent algorithm is used for training neural networks, and we will remain silent about its role in the formation of inductive bias. We will focus on the inductive bias that the model receives from its specific architecture and training data.

So, we have realized that inductive bias can be introduced into a model in various ways — by manipulating the model architecture, data, and the way it is trained. The key when designing a machine learning model is to figure out how to convey the necessary prior information about the data to the model so that it receives the desired inductive bias.

Inductive bias and size of training data

Above, we discussed that it is also possible to introduce inductive bias into the model through training data. Now, note that the larger and more diverse the training data, the more knowledge about the nature of the data the model can gain during training. Consequently, the model is less likely to choose a “bad” generalization method that will perform poorly on samples outside the training data.

In short, the more data there is, the better the model can fit. Conversely, the less data there is, the more likely the model is to choose a poor generalization method.

You probably know that neural networks often overfit when the training set is small. For example, when solving the problem of classifying images of cats and dogs, neural networks sometimes tend to pay attention to the background rather than the animals themselves. Overfitting of a model is nothing more than choosing an unsuccessful way of generalization due to the lack of sufficient information in the training data. To help the model avoid overfitting, the “knowledge” about the nature of the data that is missing in the dataset should be transferred to it in another way — for example, by introducing a stronger inductive bias into the model architecture, creating greater restrictions on the model’s structure.

Hence the conclusion: the smaller the training sample and the more complex the task, the stronger the inductive bias needs to be embedded in the model’s structure. In other words, in the absence of data, we need to impose greater restrictions on the model so that it does not “go too far off course.”

By the way, why can people, unlike neural networks, quickly learn the task of classifying cats and dogs with only a dozen pictures in the training set? It is because people have an inductive bias. We know that there are such things as background and object in a picture. And we know that when we classify pictures, we need to pay attention only to the object itself. But a neural network does not know about the notions of “background” and “object” before training — it is simply given different pictures and asked to learn to distinguish them.

Let’s see the principle “the less data there is, the stronger the inductive bias needed in the neural network architecture” in action using an example. To do this, let’s consider two neural network architectures for working with images: Convolutional Neural Networks (CNNs) and Vision Transformers (ViTs). Let’s understand how their success is related to inductive biases and what the difference is in their image processing principles.

Inductive bias of convolution layer

Let’s consider a convolution layer:

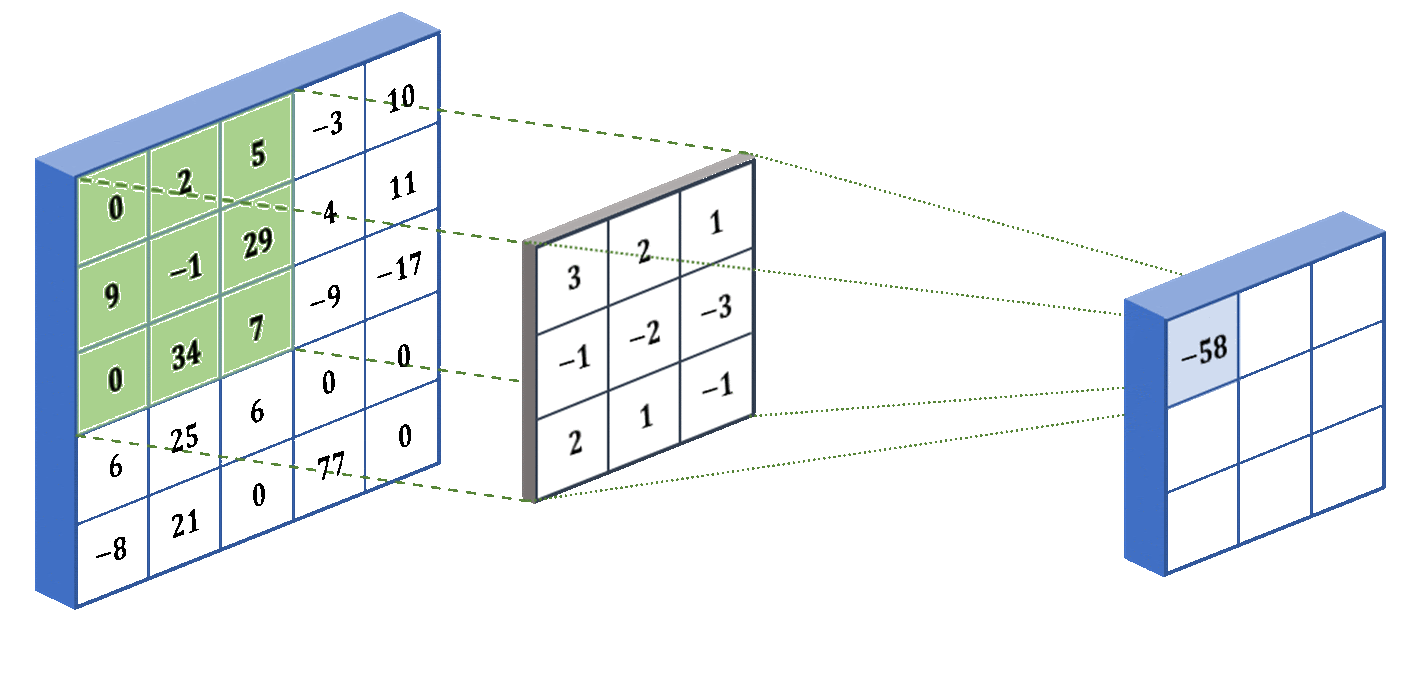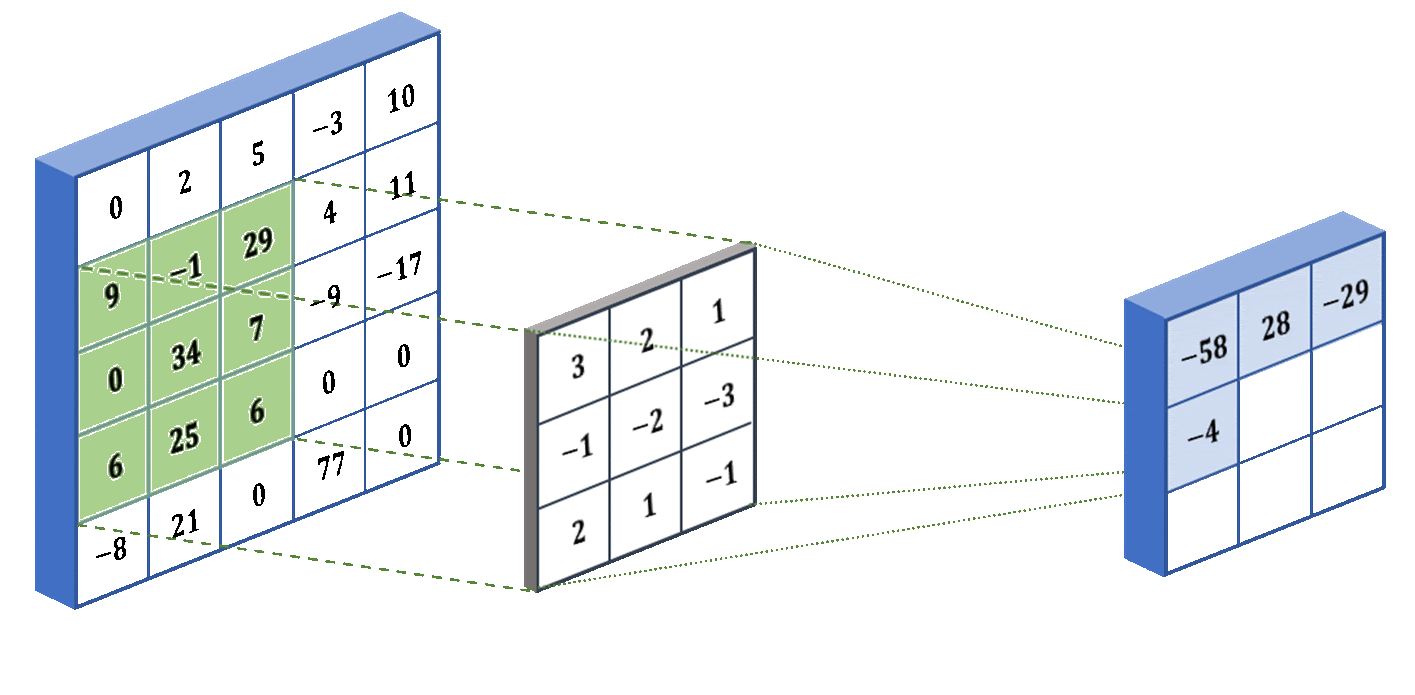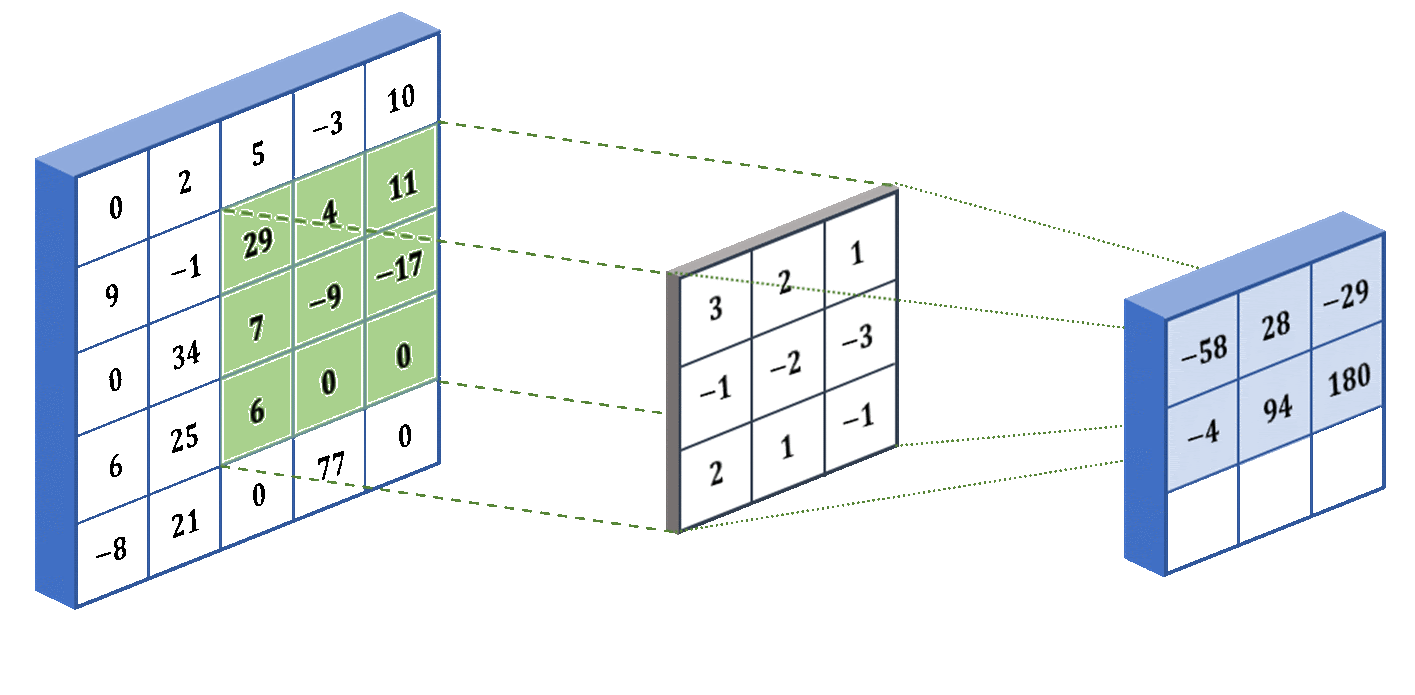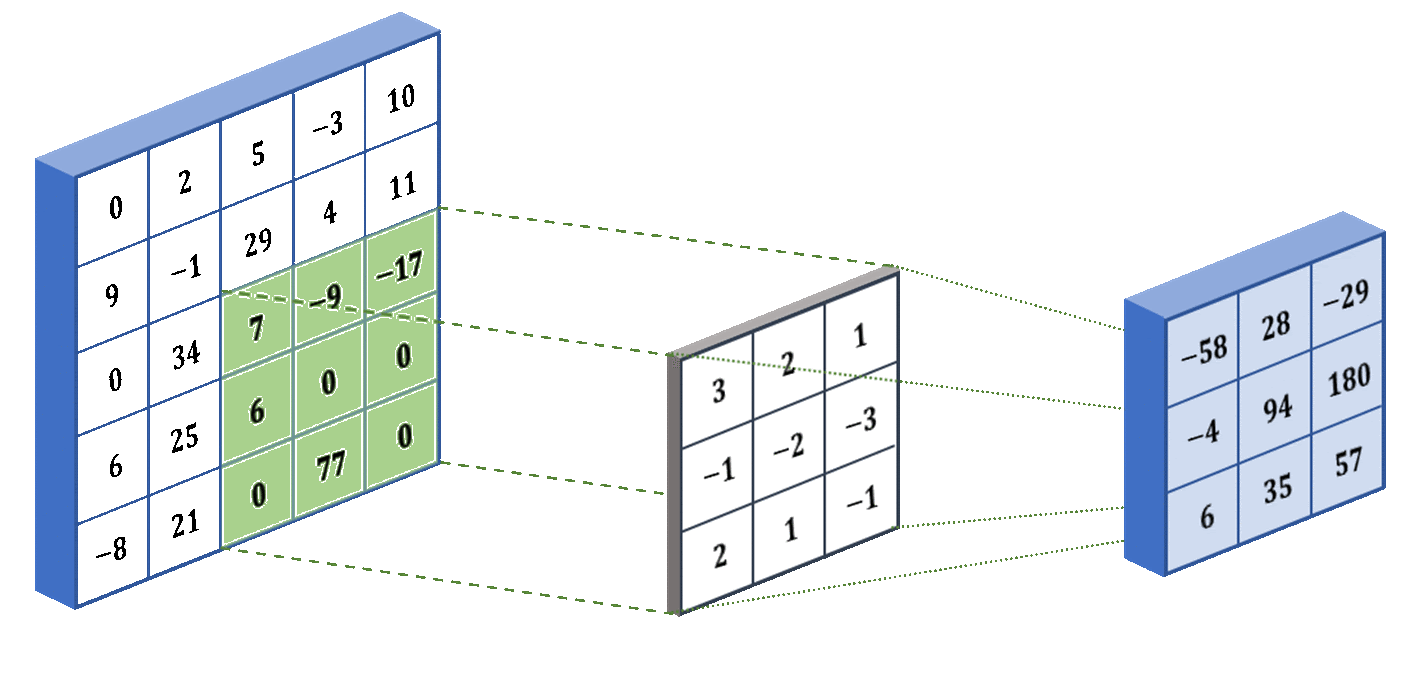
The illustration of convolution operation (https://brandinho.github.io/mario-ppo/)

Two of the inductive biases of a convolutional layer are the assumption of compactness and translation invariance. The convolution filter is designed in such a way that it captures a compact part of the entire image at a time (for example, a 3x3 pixel square, as shown in the gif), ignoring the distant pixels of the image. Also, in a convolutional layer, the same filter is used to process the entire image (as in the gif — the same filter processes all 3x3 squares of the image).

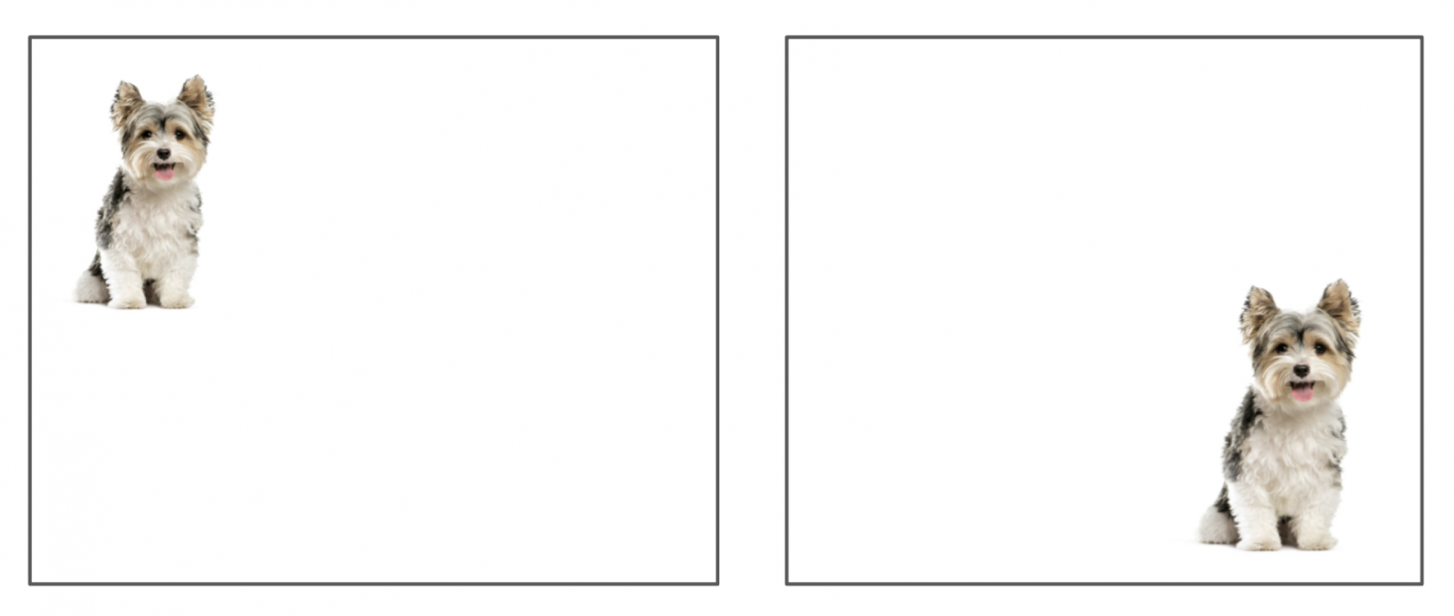
These inductive biases help Convolutional Neural Networks (CNNs) process images in a way that humans “process” them. The compactness assumption corresponds to the human idea that each object in an image is located compactly, i.e., in a certain region of the image, and not sparsely across the entire area of the image. And the insensitivity to shifts makes the neural network process the same object in the image in the same way, regardless of where it is located in the image (see the figure below).

The object in the picture (a dog) is located compactly. Additionally, we want to get the same result when processing both pictures with a convolutional neural network (for example, the answer in the classification task that the picture is a dog).

So, it turns out that the convolutional layer is designed in such a way that its inductive bias is perfectly aligned with the nature of images and the objects appearing in them, which is why convolutional neural networks are so good at processing images.

Okay, but what inductive biases do other layers have, such as recurrent, fully connected, etc.? I’d suggest that you think about it yourself =) Now, let’s mention a phenomenon called “hidden inductive bias” (or “implicit inductive bias”).

Implicit inductive bias

It often happens that neural network architecture or training data impose not only the desired, “good” inductive biases, but also “hidden” ones — those that no one consciously intended to put into the model and which are difficult to detect at first glance. Researchers conduct many experiments with neural networks, trying to identify the presence and nature of such hidden effects.

An example of such implicit inductive bias in convolutions: CNNs were built to have the two inductive biases described above — the compactness assumption and the translation-invariance assumption. These biases are the ones that humans wanted to put into convolutional networks, and they are clearly generated by the structure of the convolution operation itself. But it turns out that, in addition to these two inductive biases, the convolution architecture generates others that are not so easy to detect just by looking at how the convolution operation works.

For example, this study showed that convolutions have an inductive bias related to image texture: it turns out that CNNs tend to pay more attention to textures than to the shapes of objects when processing images. This is an example of harmful inductive bias, and we would like it to be the other way around — i.e., we’d like our neural network to draw conclusions based not on textures, but on the shapes of objects. Because of this “bias” towards textures, convolutional networks are bad at recognizing images in which the textures of an object are very different from the textures of those images in the training set.

One way of addressing this undesirable behavior of convolutions is to introduce another inductive bias into the neural network, which will make the model pay more attention to the shapes of objects, rather than their textures. This inductive bias can be introduced by changing the training data, rather than the model architecture. Images from the training dataset are augmented so that the dataset contains more images of the same shape (for example, pictures of elephants), but with different types of textures (see the figure below).

An example of augmenting training set images to reduce the influence of image texture on CNN performance. On the left is the original image; on the right are augmented versions of the left image with different textures but the same shape (https://arxiv.org/pdf/1811.12231.pdf)

This is another example of how different inductive biases can be introduced into a model through different techniques — not just by changing the model architecture, but also by manipulating the training data. It is also an example of how the presence of any inductive bias depends not on a single component — the model architecture, the data structure, or the training algorithm — but on all of them together.

Knowledge of what hidden inductive biases a model has helps you better understand how the model processes the data. It also helps make the model more effective if the hidden inductive biases you discover turn out to be harmful.

So, we’ve seen how inductive bias in convolutional layers helps CNNs process images efficiently. Now, let’s look at another neural network architecture for working with images, the Vision Transformer (ViT), and see how its recent success is related to inductive bias.

Vision Transformer and Inductive bias

The Vision Transformer is a non-convolutional neural network architecture for image processing that performs better than convolutional networks on some tasks. For example, on the image classification task in the JFT-300M dataset, which contains 300 million images.

The Vision Transformer model is based on the same idea as the Transformer architecture from the field of Natural Language Processing (NLP): the Attention mechanism. In essence, Vision Transformer is an adaptation of the vanilla Transformer model to the image domain. The model was proposed relatively recently — in 2020 — but has already gained popularity, been widely used in various tasks, and is considered a “CNN killer.”

Let’s discuss whether Vision Transformers really work better than convolutions, whether convolutions are really no longer needed, and what inductive bias has to do with all of this.

Since the Vision Transformer has no convolutions, this architecture also lacks the inductive biases of CNNs. At the same time, of course, the Transformer does have some inductive bias — as we have seen above, it is impossible to create a neural network without them at all.

The Vision Transformer is almost entirely based on the attention mechanism, so the model inherits the inductive biases associated with attention. One of these is a preference for simple functions. Like convolutions and all neural networks in general, Transformers have hidden inductive biases, and many of them are still unknown: research is ongoing to identify them. Here, for example, is a link to one such study. In general, there is still a lot of research to be done on Transformers, but what can be said for sure is that the inductive bias of a Transformer is much simpler than that of CNNs; it imposes fewer restrictions on the model.

Fewer constraints on the model give Vision Transformers more freedom to choose the best way to generalize during training. And when trained on very large datasets like JFT-300M, Transformers actually do perform better than CNNs. There are enough images in JFT-300M for a neural network with very light inductive bias to fit the task well and avoid choosing the “wrong” way to generalize.

BBut on smaller datasets (like ImageNet), the Vision Transformer shows worse performance than classic CNNs. The graph below shows the results of several models trained on different datasets: ImageNet (~1.2 million images), ImageNet21K (~15 million images), and JFT-300M (~300 million images).

Here, BiT is a CNN based on ResNet, and ViT is a Vision Transformer architecture. The graph shows that Transformers start to show better results than CNNs only on large datasets.

https://arxiv.org/pdf/2010.11929.pdf

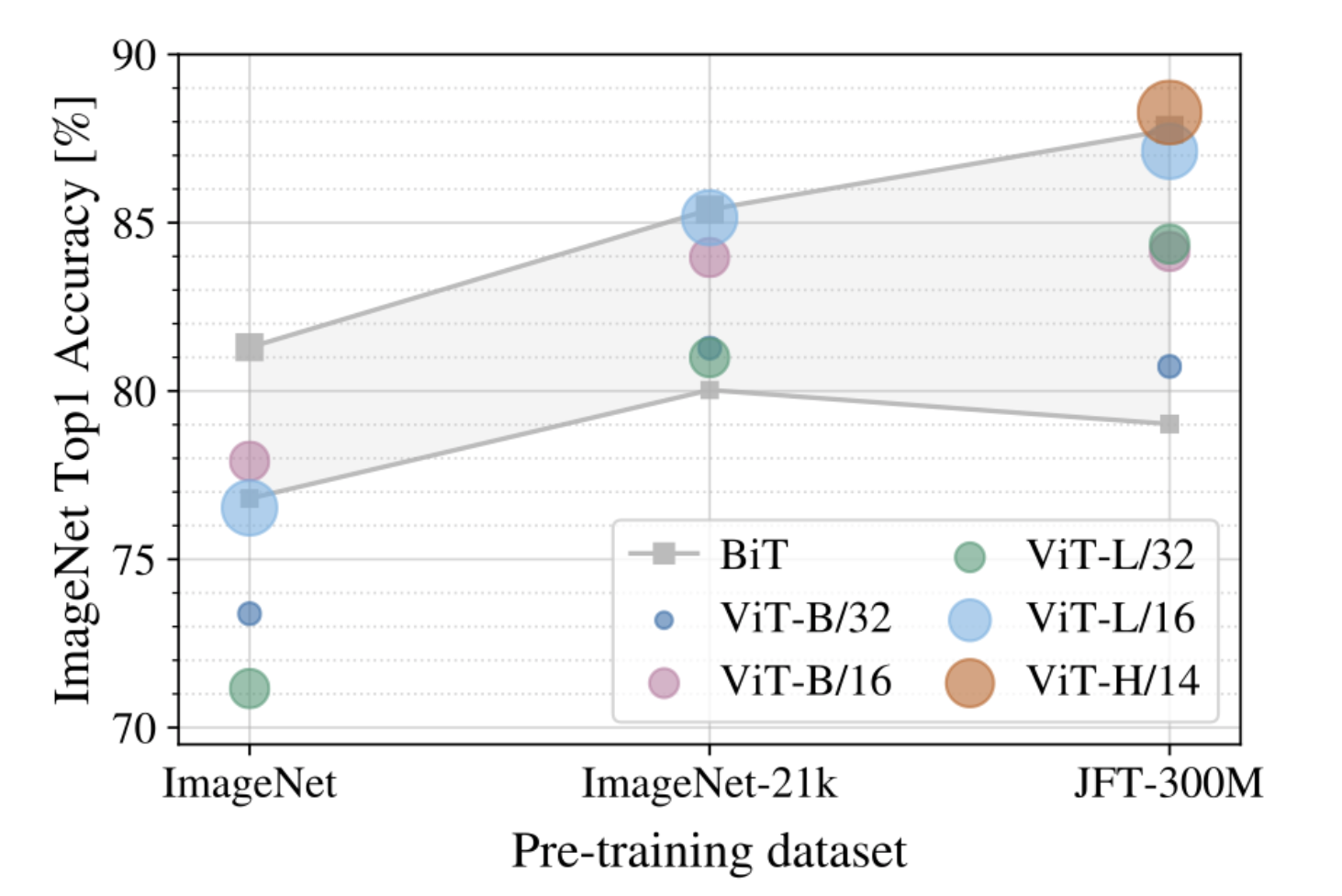
In other words, if you have a huge dataset to train the network on, a Transformer is your choice. But for training on small datasets, convolutions are still a better choice.

The advantage of the Vision Transformer over CNNs on large datasets is explained by the fact that the Vision Transformer architecture does not have the inductive bias that a convolutional layer has. Here, we see confirmation of the idea that the smaller the training dataset, the stronger the inductive bias needed to successfully train the model. But the opposite is also true: the larger the dataset we have at our disposal, the smaller the inductive bias required, and the better the model can fit the data (because it has fewer limiting biases, and the size of the dataset allows it to get all the necessary information for good generalization).

We also see that the inductive bias of CNNs really helps a lot in solving problems related to images.

Convolutions + Transformers

Above, we have discussed two approaches to image processing with neural networks: using CNNs and Transformers. Both approaches have advantages and disadvantages. Convolutions have a strong inductive bias, and they show good generalization ability on small datasets. Transformers, on the other hand, can show better results in image processing than CNNs, but they require a lot of data for this.

The team at Meta AI decided to use the best of both worlds: combining the Transformer and CNN architectures. The hybrid ConViT model will be able to process images almost as well as Transformers, while requiring less data for training. Here’s a paper describing the proposed model and why it should work (it mentions inductive bias there!).

The well-known Latent Diffusion model for generating images based on text prompts also uses both convolutions and Transformers inside.

I hope this dive into the structure of convolutions and Transformers helped to better understand the concept of inductive bias =)

Conclusion

So, it is basically impossible to create a model without inductive bias, since the very structure of the model limits its capabilities and generates inductive bias. And there is no need to create such a model: as we understood, inductive bias often helps in solving problems. The only question is how strong an inductive bias is needed to solve a specific problem, what exact form it should take, and how to design a model architecture that will have the required inductive biases (while minimizing harmful hidden biases).

The main task when creating the architecture of a machine learning model is to provide the model with an inductive bias that helps it solve the given task (as in the case of convolutions), without limiting the model too much. In fact, the task of finding new effective neural network architectures consists of designing such inductive biases.

I hope this article helped you understand what inductive bias is and why it is useful, not harmful =) Here are some more useful links on the topic:

Bibliography